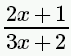Please note that this is a work in progress! I have added blocks that I just happen to have been using since I started writing this post, so they are not necessarily being added ‘simplest’ first. I will continue to add more as and when I use them.
After declaring all of the variables in an assessment item in a QTI XML file, the next step is to do the template processing. This is where variables are set or randomised, answers are calculated etc. There are too many possibilities for this section to get anywhere near specifying everything that is possible, and I won’t cover what can be done using Maxima in this post, but hopefully some of the blocks of code here can be used as they are, or will act as good starting points for doing other things.
templateProcessing Start and End
<templateProcessing>
<!-- Template processing goes here -->
</templateProcessing>
Set Fixed values
Setting a Fixed Integer value
<setTemplateValue identifier="iA">
<baseValue baseType="integer">2</baseValue>
</setTemplateValue>
Setting a Fixed Float value
<setTemplateValue identifier="fFloat">
<baseValue baseType="float">3.14159</baseValue>
</setTemplateValue>
Set Randomised values
Set a positive Randomised Integer value from a range
<setTemplateValue identifier="iA">
<randomInteger min="2" max="9"/>
</setTemplateValue>
Set a positive or negative Randomised Integer value from a range
<setTemplateValue identifier="iC">
<product>
<randomInteger min="1" max="10"/>
<randomInteger min="-1" max="1" step="2"/>
</product>
</setTemplateValue>
Note that the step attribute means that the second randomInteger will be selected only every other number in the specified range. In this case, that means it can only be -1 or 1, and not 0, so this defines whether the value is positive or negative.
Set an integer to a random value from within a range
<setTemplateValue identifier="iB">
<random>
<multiple>
<baseValue baseType="integer">2</baseValue>
<baseValue baseType="integer">3</baseValue>
<baseValue baseType="integer">5</baseValue>
<baseValue baseType="integer">8</baseValue>
<baseValue baseType="integer">13</baseValue>
<baseValue baseType="integer">21</baseValue>
</multiple>
</random>
</setTemplateValue>
Rounding
Round to a number of significant figures
<setTemplateValue identifier="fFloatRounded">
<roundTo roundingMode="significantFigures" figures="3">
<variable identifier="fFloat"/>
</roundTo>
</setTemplateValue>
Round to a number of decimal places
<setTemplateValue identifier="fFloatRounded">
<roundTo roundingMode="decimalPlaces" figures="2">
<variable identifier="fFloat"/>
</roundTo>
</setTemplateValue>
Constraints
Set a value to not equal a fixed value
<templateConstraint>
<not>
<equal toleranceMode="exact">
<variable identifier="iA"/>
<baseValue baseType="integer">7</baseValue>
</equal>
</not>
</templateConstraint>
Ensure Greatest Common Denomiator of 2 values is 1 (i.e. the values share no common factors other than 1)
<templateConstraint>
<equal toleranceMode="exact">
<gcd>
<variable identifier="iA"/>
<variable identifier="iB"/>
</gcd>
<baseValue baseType="integer">1</baseValue>
</equal>
</templateConstraint>
Ensure 2 values are not equal
<templateConstraint>
<not>
<equal toleranceMode="exact">
<variable identifier="iA"/>
<variable identifier="iB"/>
</equal>
</not>
</templateConstraint>
Ensure one value is larger than another
<templateConstraint>
<gt>
<variable identifier="iB"/>
<variable identifier="iC"/>
</gt>
</templateConstraint>
Constraint to ensure a – (b + c) != 0, i.e. a != (b + c)
<templateConstraint>
<not>
<equal toleranceMode="exact">
<subtract>
<variable identifier="iA"/>
<sum>
<variable identifier="iB"/>
<variable identifier="iC"/>
</sum>
</subtract>
<baseValue baseType="integer">0</baseValue>
</equal>
</not>
</templateConstraint>
Conditions
Set iB to equal 6, 8 or 10 if iA < 5, otherwise iB equal to 2, 4 or 6
<templateCondition>
<templateIf>
<lt>
<variable identifier="iA"/>
<baseValue baseType="integer">5</baseValue>
</lt>
<setTemplateValue identifier="iB">
<randomInteger min="6" max="10" step="2"/>
</setTemplateValue>
</templateIf>
<templateElse>
<setTemplateValue identifier="iB">
<randomInteger min="2" max="6" step="2"/>
</setTemplateValue>
</templateElse>
</templateCondition>
Constants
<mathConstant name="pi"/>
Maxima Script Dummy Variable
I won’t cover what is possible with Maxima and hence what goes in this variable, but this is the code used for setting the dummy variable:
<setTemplateValue identifier="tDummy">
<customOperator class="org.qtitools.mathassess.ScriptRule" ma:syntax="text/x-maxima">
<baseValue baseType="string"><![CDATA[
mAns : ev(iA*x^2iB,simp);
]]></baseValue>
</customOperator>
</setTemplateValue>