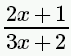Tag: guide

Here’s the link to the Help Guide for Maths Entry Questions, if you’ve come here looking for that. This post explains why we’ve created that guide.

We’re starting to deliver Maths questions online using QTIWorks, and are putting together a help guide for users, as it is not always easy to know how to correctly represent mathematical expressions in a maths answer box.

The “Input Hints” provided in QTIWorks are of some help, but are perhaps not the most user friendly and could be improved by the addition of examples, and perhaps some reordering to place the simpler and more commonly used inputs nearer the top of the list.

To supplement (/replace) this hints box, I’ve started to write a (hopefully) simple guide to using the maths input box, with some examples. This is a work in progress, so will evolve, but hopefully is a reasonable starting point. Any comments are very welcome.

This is intended as a simple guide to entering mathematical expressions as answers to questions delivered using QTIWorks. Any comments about its usefulness/helpfulness would be most welcome.

Note that you can also view an input hints box by clicking on the blue question mark symbol  next to the maths input box. You can also watch a brief video showing you how to enter mathematical answers.

This guide contains the following sections:

• The Maths Input box
• Basic Operators (+ – * / =)
• Other Operators (± > ≥ < ≤ ≠)
• Precedence (order of operations)
• Special Symbols and Functions
• Fractions (a/b)
• Brackets (a(b+c))
• Powers (x^a)
• Roots (sqrt(x) or x^(a/b))
• Subscripts (x_a)
• “Sorry, I could not make sense of your input”

The Maths Input box ^ Top

When a mathematical expression is required as an answer to a question, a text box within a larger grey box is shown. When text is typed into the text box, it is interpreted mathematically, and the resulting mathematical expression is shown:

If you click on the blue question mark symbol , an input hints box will pop up.

Basic Operators (+ – * / =) ^ Top

The basic mathematical operators can be represented by words or symbols, as shown in the table below.

Operation	Symbol	Word
Addition	+
Subtraction	–
Multiplication†	*	times
Division	/	divide
Equals	=

^†note that multiplication is implied between a coefficient and a variable, e.g. 2x = 2*x, and between consecutive variables, i.e. letters, unless the letters make up a special character, e.g. pa = p*a, but pi = π, not p*i.

Other Operators (± > ≥ < ≤ ≠) ^ Top

Other operatores, e.g. comparison operators, can be represented as shown in the table below.

Operation	Input	Interpretation
Plus or minus	+-	±
Greater than	>	>
Greater than or equal to	>=	≥
Less than	<	<
Less than or equal to	<=	≤
Not equal	!=	≠

Precedence (order of operations) ^ Top

The order of precedence, i.e. the order in which operations are performed/interpreted, follows the usual rules:

1. brackets
2. roots and exponentials
3. multiplication and division
4. addition and subtraction

Input	Interpretation	Notes
2+3*4		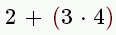equals 14
2+(3*4)		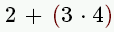equals 14, brackets are unnecessary
(2+3)*4		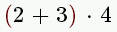equals 20, brackets are required

Special Symbols and Functions ^ Top

Generally, letters just represent variables, and multiplication between consecutive letters is implied (see Basic Operations above). However, there are certain letters or words that have special meaning, as follows:

Letter/Word	Meaning
e	e, the natural exponential, 2.71828…
i	the imaginary number, √-1
alpha…lambda…pi…etc	Greek letters, α, λ, π etc
log	logarithm function
ln	natural logarithm function
sin, cos, tan	trigonometric functions
cap, cup, in, not, notin, subset, subseteq, to, vee, wedge…and probably others	Logic and Set Theory operators

Fractions (a/b) ^ Top

Use the divide symbol,  ‘/’, between the numerator (top) denominator (bottom) of a fraction. Brackets may be needed to give the correct numerator and denominator.

Input	Interpretation
1/2
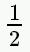2x+1/3x+2
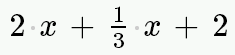(2x+1)/(3x+2)

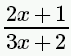Brackets (a(b+c)) ^ Top

Brackets can be used as they normally would when writing an expression.

Input	Interpretation	Notes
sin(2x+30)		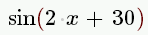brackets not needed for sin of single value, e.g. sinx gives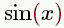
5(x+1)(2x-3)
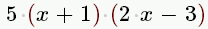3(2x-(2-y))		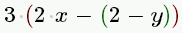equivalent to 3(2x-2+y)

Powers (x^a) ^ Top

Use ^ (hat/caret symbol) to represent powers:

Input	Interpretation	Notes
x^2
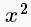x^(1/3)		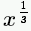fractional powers need brackets
x^-1		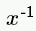negative powers do not need brackets
e^(x(2x+1))
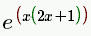e^x(2x+1)

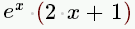Roots (sqrt(x) or x^(a/b)) ^ Top

Only a square root can be represented with the root symbol. All other roots must be represented as fractional powers:

Root	Input	Interpretation
Square root (√x)	sqrtx or sqrt(x)
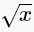Cube root (∛x)	x^(1/3)

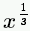Subscripts (x_a) ^ Top

Use _ (underscore) to give a subscript (similar to using ^ for powers/superscripts)

Input	Interpretation
x_1
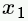y_a

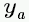“Sorry, I could not make sense of your input” ^ Top

You will see this message in a number of situations (including, but not limited to):

• When you have an operator (e.g. + – * / ^ _ =), that does not have a value/variable before and/or after it, e.g. ‘1+’, ‘*3’, ‘x/’, ‘y^’
• When you have two consecutive operators, e.g. ‘+*’
• When you have opened a bracket and not (yet) closed it, e.g. ‘2(x+3’

If you see this message when you believe you have entered a complete expression, make sure you check your expression carefully, in particular that you have closed all brackets.